728x90
📌 문제
문제) 계단 오르기
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.
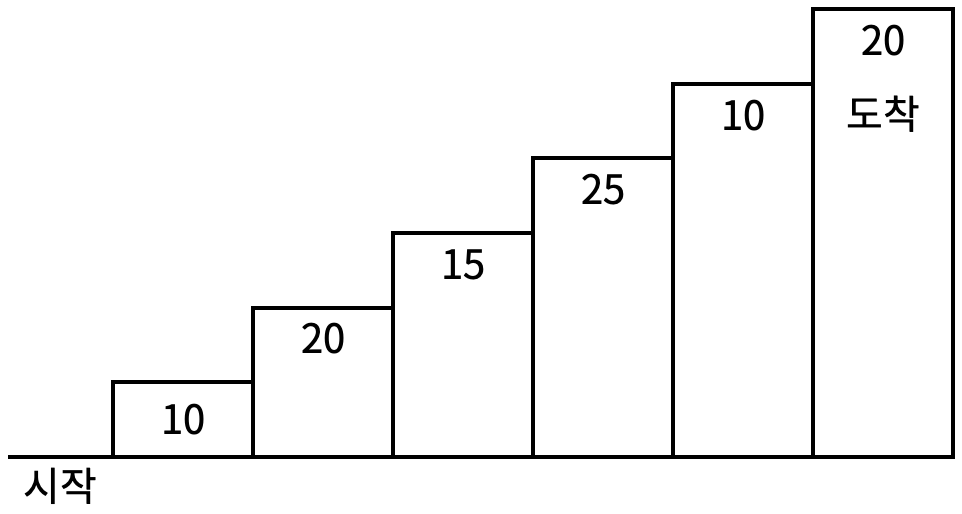
예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.

계단 오르는 데는 다음과 같은 규칙이 있다.
1. 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다.
즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
2. 연속된 세 개의 계단을 모두 밟아서는 안 된다.
단, 시작점은 계단에 포함되지 않는다.
3. 마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다.
하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
입력)
입력의 첫째 줄에 계단의 개수가 주어진다. 둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
출력)
첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.

📌 문제 분석❗️
우선 계단을 모두 올랐을 때에 총 점수의 최댓값을 구하는 문제이기 때문에 이전의 최대값을 저장하는 dp를 사용해서 푼다.
당장에 dp의 점화식이 생각나지 않더라도 조합을 좀 쓰다보면 점화식이 보인다.
dp[i]는 각 계단 위치에서 구할 수 있는 최대 점수가 들어간다.
시작점은 계단에 포함되지 않는다.
그래서 dp 배열을 선언해줄 때 N+1만큼 공간을 할당해준다.
dp[i]의 값은
순차적으로 구해보기
i = 0일 때 → dp[0] = 0
i = 1일 때 → dp[1] = stairs[1]
i = 2일 때 → dp[2] = stairs[2] + dp[1]
여기까지는 유추하기 쉽다.

i = 3일 때는 두가지 경우가 있다.
1. dp[0] + stairs[2] + stairs[3]
2. dp[1] + stairs[3]

i = 4일 때도 두가지 경우다.
1. dp[1] + stairs[3] + stairs[4]
2. dp[2] + stairs[4]
따라서 점화식은 다음과 같이 나타낼 수 있다. (i > 2)
dp[i] = Math.max(dp[i-3] + stairs[i-1] + stairs[i], dp[i-2] + stairs[i])
📌 진행
입력 값 받기
N = readInt();
dp = new int[N + 1];
stairs = new int[N + 1];
for (int i = 1; i <= N; i++) {
stairs[i] = readInt();
}
for (int i = 1; i <= N; i++) {
stairsDp(i);
}
stairs 값을 입력받고 i는 1부터 dp 메서드를 실행해준다.
dp 메서드 구현
private static void stairsDp(int i) {
if (i == 1) dp[1] = stairs[1];
else if (i == 2) dp[2] = dp[1] + stairs[2];
else if (i > 2) dp[i] = Math.max(dp[i-2] + stairs[i], dp[i-3] + stairs[i-1] + stairs[i]);
}
edge code(i = 1, i = 2)
나머지는 위의 점화식 그대로 구현해준다.
📌 전체 코드
package level16_동적계획법1_.Q8_2579;
import java.io.IOException;
public class Main {
private static int[] dp;
private static int[] stairs;
private static int N;
public static void main(String[] args) throws IOException {
N = readInt();
dp = new int[N + 1];
stairs = new int[N + 1];
for (int i = 1; i <= N; i++) {
stairs[i] = readInt();
}
for (int i = 1; i <= N; i++) {
stairsDp(i);
}
System.out.println(dp[N]);
}
private static void stairsDp(int i) {
if (i == 1) dp[1] = stairs[1];
else if (i == 2) dp[2] = dp[1] + stairs[2];
else if (i > 2) dp[i] = Math.max(dp[i-2] + stairs[i], dp[i-3] + stairs[i-1] + stairs[i]);
}
private static int readInt() throws IOException {
boolean isNegative = false;
int value = 0;
while (true) {
int input = System.in.read();
if (input == ' ' || input == '\n')
return (isNegative) ? -1 * value : value;
else if (input == '-') isNegative = true;
else value = value * 10 + (input - 48);
}
}
}




댓글